The image represents what geometric construction?
Mar 12, 2021 — Final answer: The image represents the construction of Perpendicular bisector and midpoint. Explanation: The image represents the construction
Why are circles important in construction?
Besides in math they are used in architecture and art. For example, making circular buildings involves being able to find the area of a circle. This is important because it makes sure the building is the right size and geometrically secure.
Why is the radius important with constructions?
In essence, the radius of curvature tells us how curved a curve is (Figure 1). The larger the dome, the less curve, the flatter the concrete. If any three points are chosen on an arc, the center of the sphere that would rotate through the arc can then be determined (Figure 2).
Why are circles so important in geometry?
Because circles are a group of points of equal distance originating from a center point, it's possible to determine angles and lines within a circle.
What is the construction of circle?



Just some free energy geometric construction. 🤓🤓🤓 pic.twitter.com/DsIevqzuv2
— Alfredo Canziani (@alfcnz) April 4, 2022
What is a construction in math?
"Construction" in Geometry means to draw shapes, angles or lines accurately. These constructions use only compass, straightedge (a ruler, but not using the numbers) and a pencil.
Frequently Asked Questions
What is construction in math year 7?
Students are learning about Constructions at this point in Year 7 because it is a fun Geometry topic which contrasts with the Geometry they will have learnt at Primary School. It also serves as a chance for students to learn how to use a pair of compasses.
What are the 4 types of construction?
The four main types of construction are: residential construction, commercial construction, industrial construction, and infrastructure construction.
What does geometry mean in construction?
Geometric Construction
It is the drawing of lines, angles, and shapes using only a pen or pencil, compass, and a straight edge.
What grade is geometric construction?
You'll find lessons on drawing polygons and diagonals of polygons, using a protractor to measure angles, constructing triangles and other related topics.
How do you solve for adding angles?
Okay i could add 125 by 36 to get 161.. So angle a which would be both of these angles. Together measures 161 degrees okay let's take a look at this problem. Okay.
How do you add two angles together?
A. So now that I know what's the measurement let's put the measurement down here. Now what I need to do let's give a different measurement for B.
How to do construction angles?
- Step 1: Draw a line segment AB.
- Step 2: Now place the center of the protractor on point A, such that the line segment AB is aligned with the line of the protractor.
- Step 3: Starting from 0 (in the protractor) mark the point C in the paper as per the required angle.
How to do angle measures in geometry?
With the device here. And then what you do is you look at where the other ray kind of cuts into it and you you read the measurement. Right off of the protractor. This is called a protractor.
Do angles add up to 180 or 360?
Hear this out loudPauseFor any polygon, the total degrees in the interior angles equals 180(n−2). A three-sided polygon has 180 degrees. A four-sided one has 360.
How are a straightedge and compass used to make basic construction?
The straightedge is used to draw the line (or line segment) between any two points. The compass can be used to draw circles (or circular arcs) with center at a given point, passing through any other point. But it can also be used to duplicate lengths.
What are the 4 basic constructions in geometry?
- Copying a line segment.
- Copying an angle.
- Creating a perpendicular bisector.
- Creating an angle bisector.
- Creating parallel lines.
- Creating a perpendicular line through a given point.
FAQ
- Which type of construction does this figure show that we can use a compass to draw circles to create?
A compass is used to make circles and arcs in geometric constructions. A rough sketch by hand is considered a geometric construction. Geometric constructions are created with a compass and straightedge.
- Are geometric constructions created with a compass and straightedge?
"Construction" in Geometry means to draw shapes, angles or lines accurately. These constructions use only compass, straightedge (a ruler, but not using the numbers) and a pencil.
- What constructions is impossible using only a compass and straightedge?
I would like to know the three ancient impossible constructions problems using only a compass and a straight edge of Euclidean Geometry. The three problems are: Trisecting an angle (dividing a given angle into three equal angles), Squaring a circle (constructing a square with the same area as a given circle), and.
- How do you construct the same angle?
- Following steps are used in constructing a congruent angle to the given angle.
- > Draw a ray using the straight edge.
- > Set the compass to any length.
- > Draw an arc that crosses both rays of the original angle.
- > Draw the same arc on your transfer angle.
- > Use your compass to measure the distance JK.
- >
- How do you copy an acute angle?
You're going to move the needle down to K Prime. And you're going to copy cat. Exactly what you just it now you don't have another side to go through but you want to estimate.
- Which is the best tool to use to copy an angle geometry?
Draw another line segment and copy it with a compass and straightedge. Draw an angle and copy it with a compass and straightedge. Draw another angle and copy it with a compass and straightedge. Use your straightedge to draw a triangle.
- What is the same angle rule?
- If two angles are supplements of the same angle (or congruent angles), then the two angles are congruent. Congruent Complements Theorem: If two angles are complements of the same angle (or congruent angles), then the two angles are congruent. All right angles are congruent.
- What are the rules for similar angles?
- Two triangles are similar if they meet one of the following criteria.
- AA. : Two pairs of corresponding angles are equal.
- SSS. : Three pairs of corresponding sides are proportional.
- SAS. : Two pairs of corresponding sides are proportional and the corresponding angles between them are equal.
- What is the use of compass in geometry construction?
Compass is one of the mathematical tools which is used to draw a geometrical figure, such as a circle. It is also used in the intersection of line segments and tools, which is used to intersect the line segment and helps to find the midpoint of the shapes.
- Why is the geometric compass important?
Galileo had invented a version of this geometrical compass a few years earlier and evidently gave copies of this manual to those who bought the compass. The compass had many uses, from performing square root calculations to determining ranges of cannons to solving surveying problems.
- Why do we use a compass and straightedge in geometry?
Nowadays, although different constructions can be made with various tools such as computer software, protractor, etc., constructions made with a compass and a straightedge are important because they force comprehension of the geometric constructions in the mind (Sezen, 2007).
The image represents what geometric construction?
| How does geometry work in construction? | Architects use geometry to study and divide space as well as draft detailed building plans. Builders and engineers rely on geometric principles to create structures safely. Designers apply geometry (along with color and scale) to make the aesthetically pleasing spaces inside. Applying geometry in design is unavoidable. |
| What is an example of geometry construction? | Other geometric constructions include how to draw a regular hexagon. The compass constructions can be applied on the same diagram. For example a 60 60 degree angle can be constructed and used to construct a 30 30 degree angle. Similarly a 90 90 degree angle can be constructed and used to construct a 45 45 degree angle. |
| What is geometric construction used for? | It is used to assist us in analyzing the problem using the figures created and then moving towards a solution. Geometric construction is used to draw the blueprint or a model to visualize the project building or anything. |
| What is the meaning of geometrical construction? | : construction employing only straightedge and compasses or effected by drawing only straight lines and circles. opposed to mechanical construction. |
| What are the types of geometric construction? | There are four types of geometric construction: points, lines, angles, and circles. |
| What is an example of geometry point in real life? | Points can be joined in different ways. A point has no dimensions, such as length, breadth or thickness. Some common examples are: a star in the sky, the tip of a compass, the sharpened end of a pencil, the pointed end of a needle, starting point of a race, corner of a bond paper, and the tip of the scissor. |
| Which one is the correct construction for a perpendicular bisector? | The steps for the construction of a perpendicular bisector of a line segment are: Step 1: Draw a line segment PQ. Step 2: Adjust the compass with a length of a little more than half of the length of PQ. Step 3: Place the compass pointer at point P and draw arcs above and below the line. |
| What is the symbol for a perpendicular bisector? | ( ⊥ ) The symbol for the perpendicular is ( ⊥ ). Let us take a look at few examples say we have two lines as shown below these two lines are perpendicular if they intersect to form a right angle. Now let us take a look at the second word Bisector. |
| What is an example of a perpendicular bisector? | A perpendicular bisector is a line, line segment, ray, or plane that divides a line segment into two equal pieces and intersects the bisected line segment at a right angle. Examples are the altitude of an isosceles triangle, and the three lines used to find the circumcenter of a triangle. |
| What is the difference between a bisector and a perpendicular bisector? | In Geometry, Bisector is a line that divides the line into two different or equal parts. Similarly a perpendicular bisector is a line which intersects a given line segment at a [{90^ circ }] degree, and also it passes through the midpoint of the line segment. |
- What are the 4 steps in constructing perpendicular bisector?
Step 1: Draw a line segment XY of any suitable length. Step 2: Take a compass, and with X as the center and with more than half of the line segment XY as width, draw arcs above and below the line segment. Step 3: Repeat the same step with Y as the center. Step 4: Label the points of intersection as 'P' and 'Q'.
- What tool should not be used to complete geometric constructions?
A geometric construction, in its purest form, never involve any numbers. Protractors contain numbers, so they are not allowed!
- What tools can be used to a make a geometric construction?
When you draw something accurately without the use of numbers, it is called geometric construction. The two tools that you need to make geometric constructions are these two: compass, straightedge.
- Which of the following is never used in geometric construction?
The correct answer is Protractor. In geometry, pencil, compass, and ruler are used to draw different shapes, angles, or lines. But the protractor is used to measure the angles. So, it can be said that the protractor is not used in geometric construction.
- What tools did the Greeks not use in geometric constructions?
Expert-Verified Answer
Using these two tools, almost any shape can be constructed. Given here: The options as Eraser, protractor, straightedge, compass. Clearly there compass, straight edge and protractor were used to construct geometrical shapes and angles. But there is no account of uses of eraser by the Greeks.
- Which geometric tools are not used when copying an angle?
Bisecting a segment and constructing the perpendicular bisector of a segment. First, remind students that there are two rules: They may only use the compass and the straight-edge tools. They cannot use the ruler to measure lengths or the protractor to measure the angles.
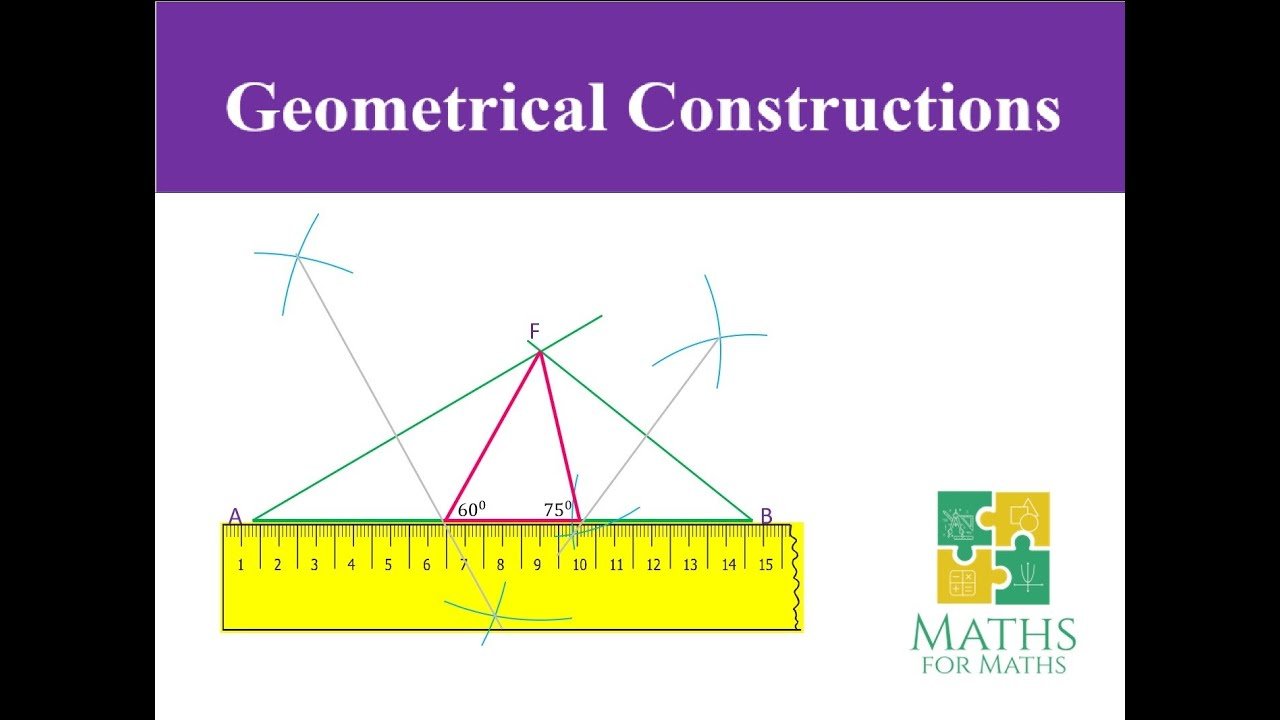
- Which construction is represtented by these construction marks
Aug 10, 2016 — Which construction is represented by the diagram? 1) copying angle A ... [Leave all construction marks.] A. B. 14. Construct a right triangle
- Does construction require geometry?
- A precast stair, steel joist or beam requires geometry to ensure proper fit when placed. The mechanical contractor uses geometry to ensure his ducts and pipes will miss columns and walls. There are many examples of geometry being used in construction.
- What is an example of construction geometry in real life?
Geometric Shapes in Daily Life
Buildings: Skyscrapers, houses, and architectural structures incorporate geometric shapes such as squares, rectangles, triangles, and circles in their design.
- What math concepts are used in construction?
In Construction, tradespeople use mathematical concepts such as measurement, geometry and trigonometry for building roofs or houses, plasterers use ratios for mixing compounds, plumbers use hydraulics for heating systems. Mathematics may not be obvious to those in the construction sector, but it's use is everywhere!
